Autumn 2016: a new academic year, a new term, time for a new module! Well, not entirely new since half of it was largely based on a module I taught the previous couple of years (but with much of the detail removed to concentrate more on the ideas and applications), but still this was a module that I have been wanting to put on for a while now so it was great to finally get the opportunity. Now term has finished, I though it was worth putting down a few thoughts about how it went while still fresh in my mind.
Autumn 2016: a new academic year, a new term, time for a new module! Well, not entirely new since half of it was largely based on a module I taught the previous couple of years (but with much of the detail removed to concentrate more on the ideas and applications), but still this was a module that I have been wanting to put on for a while now so it was great to finally get the opportunity. Now term has finished, I though it was worth putting down a few thoughts about how it went while still fresh in my mind.
MA3J3 Bifurcations, Catastrophes and Symmetry was, unsurprisingly, made up of three sections detailing how steady-state solutions to differential equations (or potential functions) change as we vary a parameter (or parameters), essentially how things that we observe around us can change, sometimes quite dramatically, as some value is changed, think a change in temperature, or applying an increasing force to something. Historically these topics are also embedded in the history of the Mathematics department at Warwick through Christopher Zeeman in the 70s and early 80s and Ian Stewart late 80s and 90s. As an undergraduate myself I took a final year module on Catastrophe Theory which went into much more of the technical detail than I intended to in this module, and more recently I taught, for many years, a module called Modelling Nature’s Nonlinearity which did cover all three topics as well as several others but in less depth than I wanted (you would always just be getting to the interesting stuff when you had to move on to the next topic). It was also nice that at the end of the module that I could almost emulate one of my favourite undergraduate lecturers, Stewart Stonehewer, who ended an enthralling Galois Theory course with the statement that there were five main results in the course, summarised as Theorems A, B, C, D and E and that there were 5 questions on the exam paper. OK, with a compulsory question and 4 others I was one short, but still. For anyone interested an indicative syllabus below, but all this mainly example driven.
Bifurcations: The basic underpinning theory for the module, preliminaries, motivating examples/demonstrations*, typical co-dimension one bifurcations (transcritical, saddle-node, pitchfork), examples of co-dimension two bifurcation, centre manifold reduction, periodic solutions via Hopf bifurcations, structural stability and a little bit of Hartman-Grobman and chaos thrown in for good measure (Lorenz Equations).
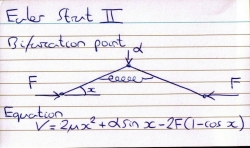
Catastrophes: Essentially sticking to “elementary” catastrophe theory to avoid controversy (see end of this list!): Euler Strut, canonical cusp catastrophe, Spruce-Budworm populations, right equivalence, co-dimension, Hadamard’s Lemma, germs, jets, versal unfoldings, bifurcation geometry of Ak singularities, Gravitational Catastrophe Machine, ship stability, Zeeman Catastrophe Machine, stock prices, discussion on the “catastrophe controversy”, Thom’s Seven Elementary Catastrophes.
Symmetry: D4-invariant functional, deformations of an elastic cube, group representations, invariance, equivariance, isotropy subgroups, fixed point subspaces, group orbits and conjugacies, axial subgroups, Liapunov Schmidt reduction, Equivariant Branching Lemma, speciation example (Sn) , brief mention of stability and restrictions on the Jacobian, Animal Gaits, spatio-temporal symmetries, twisted subgroups, coupled oscillators, Γ-simple, Equivariant Hopf Theorem, rings of cells, H/K Theorem, gaits revisited.
The module was also a little experimental in its delivery, and my first experience of lecture capture which made things more interesting, with material being uploaded to the module’s Moodle page. The lecture capture in the room I was timetabled in was restricted to video of whatever was being projected onto the screen and voice, but fortunately with six banks of blackboards to choose from and the screen only covering two of those boards it was possible for a smorgasbord of blackboards, summary file cards on the visualiser and occasionally PC for Prezi and Second Life (we are very protective of our blackboards in Warwick Maths, much to the despair of many of our colleagues elsewhere in the University). Additionally I was taking photographs of the blackboards to upload (although this started late, and was a little sporadic: end of lectures not best time to remember to take photos of current boards).
File cards on the visualiser to accompany lecture capture came about initially because I was writing draft lecture notes on them so that I could try to rearrange the order I was doing things to suit the moment (it wasn’t always clear in which order to do things, or whether to introduce examples before or after more detailed theory), but then it became clear that they could further be used during the lectures where there was still the flexibility to change the order of things on the fly which lecturing from notes does not (or at least, does not so well). Of course, a significant number of students still asked for some printed lecture notes which I am now reluctantly putting together based on the order in which I did things this year. Next year I will need to decide how to incorporate them into the delivery to keep the flexibility I have enjoyed this year,
| A selection of file cards used on visualiser for lecture capture. | ||
| Blackboard photo example. |
| Some screen shots from lecture capture. | ||
Post-mortem: I think it went well. I certainly enjoyed the challenges that lecture capture threw up, and as I said this is a module I have been wanting to put on for a long time, but it was more difficult to decide what to leave out than what to include. Previous incarnations of my Equivariant Bifurcation Theory module have certainly got carried away with some of the theory I find exciting but may have left many of the students behind, but you still need a certain amount of the theory in order to appreciate what is going on and why the examples work (and why this stuff is so goddamn amazing). Student feedback was good, fortunately most claim to have ended up with a good set of lecture notes to revise from (one of the feedback form questions) and a shout out to my TA for the support classes who also received some glowing praise. I guess the final test is how they all do on the exam next April! For next year, I feel I’ve got a solid foundation to work on, and a few tweaks where things didn’t quite work as well as I would have liked, but on the whole, very happy with it all.
*Demonstrations included the Zeeman Catastrophe Machine caught on visualiser (see screen shot above) but also Euler Strut on some perspex strips found in the department library. I probably got more excited than I should have done by the fact that with these strips you could really feel where the initial pitchfork bifurcation happens as you increase the force on the two ends with your hands which you don’t get by using a ruler. Just call me a nerd.
Picture at beginning of blog entry is of the Vasa, a Swedish warship that capsized a short while into its maiden voyage in 1628. One of the applications we discussed in the module was of ship stability and how catastrophes can occur (in the case of the Vasa both mathematically and literally).