Bifurcations in the presence of symmetry, or Equivariant Bifurcation Theory, has been one of my main interests since my PhD (thesis title “Coupled Oscillators With Internal $\mathbf{Z}_2$ Symmetry”). In layman’s terms it is the patterns you expect to see as solutions to problems when underlying rules have some symmetrical properties. More mathematically, assume we have some group $\Gamma$ acting on some vector space $V$ and we have a system of ODEs
\[ \frac{dx}{dt}=f(x,\lambda)\]
where $f:V\times R\rightarrow V$, $x \in V$ and $\lambda \in R$ is a bifrucation parameter. Equivariance under $\Gamma$ means that $f(\gamma x,\lambda)=\gamma f(x,\lambda)$ for all $\gamma\in\Gamma$. Assuming we have a trivial solution with full symmetry $\Gamma$ (every element of $\Gamma$ leaves the solution unchanged), then if a bifurcation occurs as we vary $\lambda$ then the bifurcations which occur have less symmetry, but in a very precise way (either steady-state solutions or oscillations through a Hopf bifurcation). Similar theory can be applied to potential functions which are invariant under $\Gamma$ ($g(\gamma x,\lambda)=g(x,\lambda)$).
The “bible” for this theory is Golubitsky et. al. (1988), but a more recent, and accessible, text is Golubitsky and Stewart whcih also covers advances in the area since, as well as an introduction to where the applications to networks is heading (where the symmetries of the system are no longer so obvious but can be described using groupoid formalism).
My own interests in this area concern applications and the theory of systems of coupled cells where each cell has its own inherent symmetry (how these cells are coupled can have implications on the solutions you expect to see, for example Wood (2001).
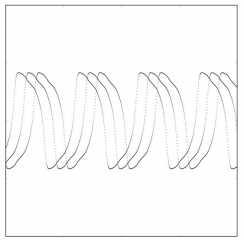
Three coupled oscillators with internal symmetries
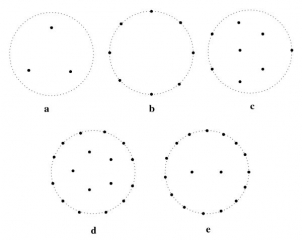
Applications include using the theory in the study of central pattern generators that control insect locomotion (see my insect locomotion page) and optimising the configuration of arrays of hydrophones Wood et. al. (2003). Hydrophones are essentially directionless underwater microphones used to detect anything from fish to submarines, in order to be able to detect the direction that sound is eminating from they are placed in arrays of up to 20 hydrophones and then there is a neat method for”steering” them towards the sound that is of interest. The question is how to place them within this array (see figure below).
Optimised hydrophone placement
References:
- M. Golubitsky, D. Schaeffer, I. Stewart, Singularities and groups in bifurcation theory, Volume 2, Springer 1988.
- M. Golubitsky, I. Stewart, The Symmetry Perspective, Birkhauser, 2003.
- D. Wood, A Cautionary Tale Of Coupling Cells With Internal Symmetries, International Journal of Bifurcation and Chaos 11, pp 123-132, 2001.
- D. Wood, D. Allwright, Optimisation Of Hydrophone Placement: A Dynamical Systems Approach, European Journal of Applied Mathematics 14, pp369-386, 2003.