Research into insect locomotion is a large and active area in both biology and engineering. From a mathematicians point of view the interest is in both trying to understand the mechanism that has evolved in insects to produce the patterns observed, and to help provide an insight to roboticists as to how to improve control mechanisms for hexapod robots (although I admit it is the former that is the driving force for my own interests).
Superficially insect locomotion, or the gait, follows a specific set of rules, see for example the seminal paper on the subject Wilson (1966) or Manton (1973) which can be summarised as follows (although there are many other excellent references with a such summary):
To ensure stability at all phases during an insect’s locomotion it must:
- have at least three legs in contact with the ground disposed about the centre of gravity;
- paired legs must move in opposite phase (except when swimming or jumping);
- leg three must remain on the ground until the footfall of leg two, and similarly for legs two and one, where legs on each side are numbered from front to back.
- the most mechanically advantageous hexapod gaits giving least strain on the organisms are those in which the footfalls occur at equal intervals of time;
- the duration of the forward swing of the leg, off the ground, remains constant as
walking speed changes.
If we label an insects legs as follows we can summarise this my bracket notation, e.g. legs within a bracket move together, and there is an equal interval of footfalls between brackets.
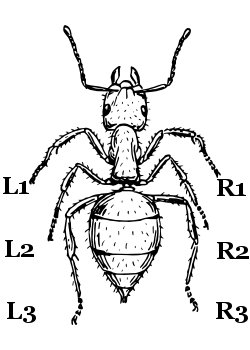
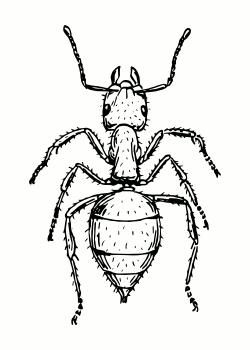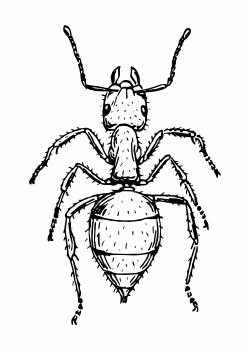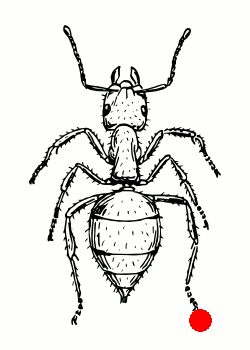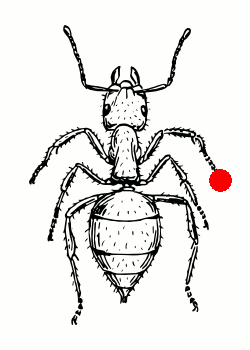
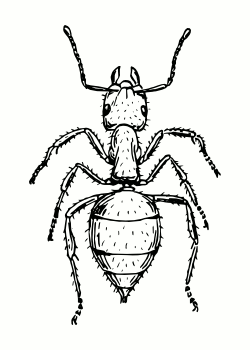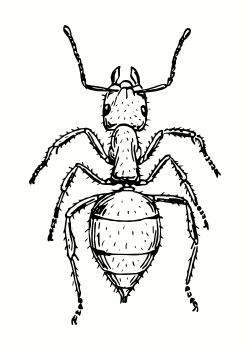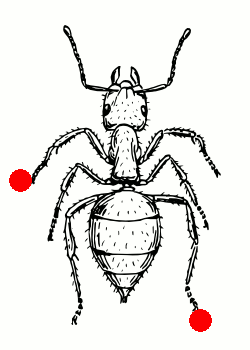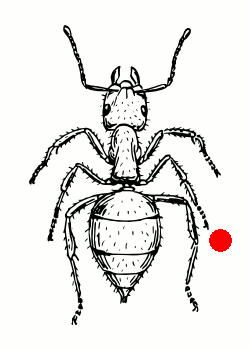
So for example, the gait (L3 R1)(L2)(L1 R3)(R2) below consists of legs L3 and R1 moving together, followed by L2 on its own, then L1 and R3 together and so on. Locomotion obeying these rules I term “ideal gaits”, for mechanical reasons they are the gaits that an insect should attempt to use for least strain on it’s body, three commonly observed such gaits are shown below.
 |
 |
 |
| Slow Metachronal | Fast Metachronal | Tripod |
| (L3)(L2)(L1)(R3)(R2)(R1) | (L3 R1)(L2)(L1 R3)(R2) | (L3 L1 R2)(R3 L2 R1) |
However a more detailed analysis of the published observations show a much wider range of variations on these rules.
The widely accepted mechanism for co-ordinating leg movement throughout the animal kingdom is the idea of a Central Patter Generator, a network of neurons that have an input from their brain to move forward, and emits signals to the muscles of the legs in the appropriate sequence to achieve this.
It can be shown that many suggested mathematical models of Central Pattern Generators consisting of only 6 oscillators, or doubling up to 12 following the work of Golubitsky at. al. on quadruped gaits although being able to generate many ideal gaits, do not allow for many of the variations seen that cannot be explained by proprioceptive feedback. The challenge is to develop models for Central Pattern Generators that remain as simple as possible, with few changing parameters to exhibit different gaits, but which better reflect the observed gaits.
Past work of mine on this topic includes an MSc. dissertation and a chapter of my PhD. Thesis. Current work in this area is both a thorough review of the available data that has been published over the past 80 years (although observations on insect gaits goes back a lot further than that) and developing a mathematical model of a Central Pattern Generator based on evolutionary considerations which better explains the observations.
References:
- S.M. Manton, The Evolution of Anthropodan Locomoting Mechanisms Part 10: Locomoting Habits, Morphology and Evolution of the Hexapod Classes, J. Linn. Soc. London, Zoology Series, 1973.
- D. Wilson, Insect Walking, Annual Review of Entomology 11, pp103-122, 1966.
- M. Golubitsky, I. Stewart, The Symmetry Perspective, Birkhauser, 2003.









